玩转仙人掌
Playing With Cactus
by VFleaKing
大家好还记得我吗
- 我就是为吕凯风配音的演员vfk~
- 今天我们来讲仙人掌!
什么是仙人掌?

仙人掌的定义
如果一个无向连通图的任意一条边最多属于一个简单环,我们就称之为仙人掌。所谓简单环即不经过重复的结点的环。
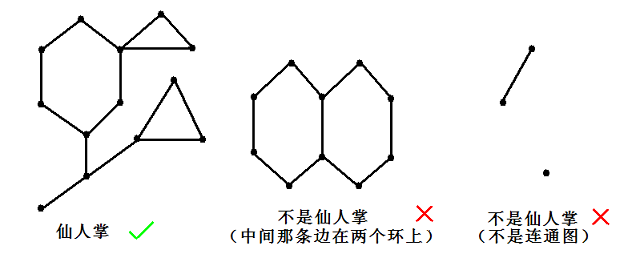
树一定是仙人掌,这意味着仙人掌的算法一定对树成立。
仙人掌的边数规模
- 对于一个 $n$ 个结点的树,最多 $n - 1$ 条边。
- 考虑一个 $n$ 个结点的仙人掌的一个生成树,每个环肯定对应一条非树边。
- 每条边肯定对应至多一个环,所以每条边肯定对应至多一个非树边。
- 所以至多 $2n - 2$ 条边。
- 好像官方定义的仙人掌不能有重边?我觉得允许重边的仙人掌更自然。
仙人掌结构
- 仙人掌有很强的树的感觉。我们可以重新定义一个结点或环的儿子和父亲。
- 对于一个结点 $v$,它的父亲可能是结点还可能是环。根结点没有父亲。
- 对于一个结点 $v$,它的儿子可能是结点还可能是环。
- 对于一个环,它的父亲是最上面的那个结点,它的儿子是环上的其它结点。
- 一个父亲不是环的结点 $v$,我们还是按树的方式定义 $v$ 的父亲结点。
- 一个父亲是环的结点 $v$,我们定义 $v$ 的父亲结点和母亲结点为环上与它相邻的两个结点。沿着环上一端的父亲结点或母亲结点可以遍历这个环。
例子
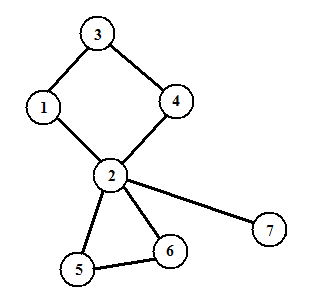
- 3 的儿子是环 3-1-2-4,当然这个环的父亲就是 3。
- 1, 2, 4 号结点的父亲是环 3-1-2-4,当然这个环的儿子就是 1, 2, 4。
- 4 的父亲结点是 2,2 的父亲结点是 1,1 的父亲结点是 3。
- 1 的母亲结点是 2,2 的母亲结点是 4,4 的母亲结点是 3。
- 2 有个两个儿子,一个是环 2-5-6,一个是结点 7。
遍历仙人掌
- 我们可以用dfs遍历仙人掌
- 当到达一个结点 $v$ 时,for每条边,无视自己的父亲。
- 如果未遍历过说明发现了自己的儿子,递归下去。
- 否则如果遍历过:
情况一

可能是已遍历的环儿子的另一个端点,此时无视。
比如在 2 号结点,我们之前从 5 号结点往下遍历了一下,当后来发现了 6 号结点时就是这样。
情况二

也可能是新发现了一个环,我们需要把这个环的所有儿子的母亲结点搞清楚。
比如在 6 号结点,当我们发现了 2 号结点时就是这样。
注意此时 6 号结点的父亲是 5,5 的父亲结点是 2,我们就可以沿着父亲结点往回走来遍历这个环。
具体细节!
- 自己脑补下就清楚了嘎嘎。
- 你可以使用访问到一个结点的时间来区分这两种情况。
判定仙人掌
- 直接在遍历仙人掌时设置母亲结点的时候判一下就行了。
随机生成一棵仙人掌
- 无脑暴力!每次随机一条边加上去,判定是否是仙人掌,不是仙人掌就不加。
- 适合生成小数据。
随机生成一棵更大的仙人掌
- 先随机生成一棵树然后dfs,每次要回溯的时候随机往祖先方向连非树边并标记被覆盖的树边。
- 往上连非树边最多能连多远这个很好搞。
- 或者索性每次以 $0.1$ 概率往上走,往停下来的地方连非树边。
- 时间复杂度显然是线性的。
- 造出来的仙人掌上一般都长满了环,碎片化工艺制造,碎玻璃艺术风,看起来再人工塞几个大环的话数据强度就非常强了。
仙人掌题对拍技能 get
- 有了随机数据生成器,就可以写个暴力和正解对拍啦!
- 下面就可以研究些更难的问题。
仙人掌的DP

- 给出一个仙人掌,求 $1$ 号结点到每个结点的距离。
- $n \leq 10^5$
裸上
- 类比树上的DP我们能搞出仙人掌的DP。
- 既然你已经能理清结构并遍历仙人掌了,那就很裸了。
- 直接从根开始往下DP,到一个结点 $v$ 时访问每个儿子:
- 如果这个儿子是个结点,那么像树一样做。
- 如果这个儿子是个环,那么我们搞搞 $v$ 到环的儿子结点的距离,然后递归环的儿子。
仙人掌的最短路查询

- 给出一个仙人掌,每次询问 $v, u$ 间的最短路。
- $n, q \leq 10^5$
- 仙人掌图上的简单路径一定是沿着普通的边走走或者在环上逛个半圈走走。
- 类比树上的最短路查询我们能搞出仙人掌的最短路查询。
- 我们还是可以像树一样定义两个结点间的最近公共祖先。
- 预处理 $2$ 的整数次幂的祖先,就能求出最近公共祖先 $a$。
- 记下从根到每个结点 $v$ 的最短距离 $d_v$。
- 如果最近公共祖先是个结点那么就是 $d_v + d_u - 2 d_a$。
- 如果是个环那么只要特别地算一算在这个环上的走法。只要预处理每个环的长度以及环的父亲结点到每个环上结点的逆时针距离就行了。
仙人掌的点分治
- 类似树的点分治,我们可以搞出仙人掌的点分治统计仙人掌上的路径信息。
- 我们每次找一个结点 $v$,求出把连向 $v$ 的边都断了并且 $v$ 所在的每一个环上的边都去掉(不去掉环上的其它结点)后最大的连通块大小。这样找出连通块最大的最小作为重心。
- 然后我们统计经过 $v$ 或 $v$ 所在的环的路径的信息。
- 然后删掉 $v$ 连出去的边和 $v$ 所在的每一个环上的边,递归各个连通块统计信息。
时间复杂度?
和树的点分治一样分析。
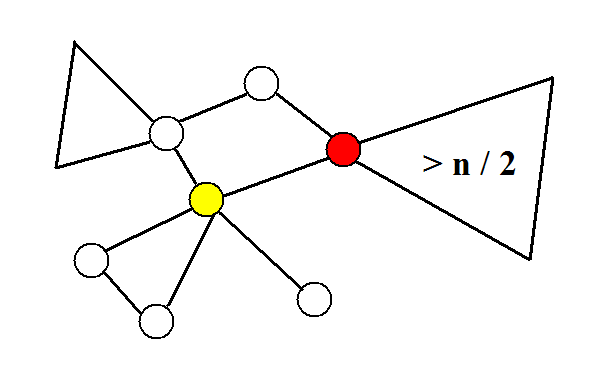
如上图,假如我选了黄点为重心,那么还不如选红点,这样会使最大的连通块大小减小。
有兴趣?
欢迎 AC UOJ Round #1 C 跳蚤国王下江南。
- 给出一个仙人掌,求从 $1$ 号结点出发经过恰好 $l$ 条边的简单路径有多少条。对 $l = 1 \dots n - 1$ 输出答案。
- $n \leq 10^5$
动态仙人掌
- 古有动态树,今能不能有动态仙人掌呢?
- 小朋友们!你们是否开始激动起来了!
动态仙人掌 0
- 每次加边,删边,查询两点是否连通。
- 对于加边,某个连通块不是仙人掌就不执行。
- $n, q \leq 10^5$ (不过这题太基础了所以我没放出来……)
强行 Link-Cut Tree 维护
- 可以发现这个问题至少是个动态树。
- 考虑把树上的边先染成白色,然后再把每一个环上的边染上黑色。
考虑加边
- 如果连接的是不同的连通块,那么直接接起来。
如果连接的是相同的连通块,那么说明是一条非树边,于是就把树上对应路径的边全部涂黑。
不过如果已经有黑边那么就说明这条边在多个环上于是就不执行。
- 考虑删边
- 如果删的是一条非树边,那么把对应的树上路径染白就行了。
- 如果删的是一条白色的树边,那么直接删。
- 如果删的是一条黑色的树边,那么就先删对应的非树边,然后再删掉这条边,最后再把原来那条非树边加回来。
动态仙人掌 I
- 每次加边,删边,查询两点间最短路。
- 对于加边,某个连通块不是仙人掌就不执行。
- $n, q \leq 10^5$
强行 Link-Cut Tree 维护
- 维护一棵生成树,在环上的树边记录对应的非树边。把不同的环染上不同的颜色。
- 对于每个环记下环的长度。
对于一条链如果链中间(不包括头尾)有一段相同的颜色,那么说明环整个地出现了,可以考虑这个环的长度和在链上出现的长度搞出最短路。
保留头尾不完整的颜色段(如果有的话),区间信息就很好合并了。
- 由于时间原因没法完全说清楚。

动态仙人掌 II
- I 基础上多输出下路径上边权长度的最小值。
强行 Link-Cut Tree 维护
- 现在信息不可减了。
对于两个相邻的树边如果颜色不同说明这里有环出去了,于是记录往外走的这个信息,我们称为拓展信息。
保留头尾不完整的颜色段和对应的环往外的拓展信息(如果有的话),区间信息就很好合并了。
- 拓展信息可以在LCT access的时候搞搞维护下。
- 由于时间原因也没法完全说清楚。

动态仙人掌 III
- II 基础上多加个给最短路上的边的整体操作。
强行 Link-Cut Tree 维护
- 强行给树边的拓展信息打标记,强行下传。
- 这个也可以LCT access的时候搞搞。
- 由于时间原因也没法完全说清楚。

- 虽然肯定是 $O(n \log n)$,但是记录的信息和标记简直多得丧心病狂。
- 不要问我这个方法好不好写!我写了整整1000行,将近24KB,你说好不好写?
Link-Cut Cactus
- 类比 Link-Cut Tree,我们不维护仙人掌的生成树,而是直接维护链剖分。
- 并且保证 access 的时候一定是沿最短路。
- 所以 access 的时候碰到结点就像 LCT 一样做,碰到环就调整成最短路再往上走。
- 类比 LCT 的证明,能保证 $O(n \log^2 n)$ 的上界。
- 反正比维护生成树要简洁多了。
丢链接跑
总结
- 营员交流给的时间太少了口亨!感觉什么也没讲。
- 不过感觉还是能感受的到,由于树是仙人掌,所以对于仙人掌的各种算法自然要对树也成立。这就导致仙人掌的算法继承了树的算法,并且进行了拓展。
- 这就是仙人掌的优美而高贵之处了。
感谢
- 感谢业界毒瘤彭雨翔同学对我的启发。
- 感谢 CCF 提供了此次营员交流的机会。
- 最后给 AC 了动态仙人掌系列的感动OI界人物点个赞。
- 谢谢大家!