前两天有良心用户 negiizhao 发现：UOJ #34 多项式乘法有 4 个测试点数据范围虽然很大，但带有特殊性质，导致按运行时间排序的排行榜上出现了一批靠特判数据性质排在前面的选手。

根据 negiizhao 在 UOJ 用户群发起的投票，有 40 票赞成更换数据，13 票反对。所以刚刚我替换掉了原来的第 3、4、11、12 号测试点，把原测试点移动到了 extra test。现在这题正在重测。

感觉这个形式很好，欢迎大家通过民主投票的方式表达自己对 UOJ 的建议哦

Hi，大家好，大家还记得我吗？

好像最近大家在 CTSC + APIO，可是我看到了十五人的成绩单的时候却发现只有几个名字我熟悉了。。。然后又后知后觉地发现 PYOJ 早就消失了。。

我可能淡出 OI 太久了吧。。。突然有点伤感

想起我 NOI 那年是 2014 年，竟然已有四年之远了 （那些年的比赛还是不会搞丢选手程序的 [滑稽]）

转眼我已经大三了。。我记得我大一的时候努力适应着大学的新生活，大二的时候立志要做点学术，大三上学期焦头烂额地找春季研修。。。渐渐地就忘记管 UOJ 什么事了。。。看到大家仍然还在孜孜不倦地交题感到很感动。

我有点怀念从前啊，所以大概想近期闲的时候稍微填一些坑，但也不知道最后会填多少。。。

以及我想调查下现在有多少人建了自己的 UOJ 诶，可以在评论区留下言吗？

测评机没内存了 [捂脸]

并不是 MLE 会爆 RE，而是程序说 “我要内存！” 结果内存表示 “我不够了！” 的时候会 RE。

有两台测评机，其中一台内存不够了，所以才造成了时而 RE 时而不 RE 的问题。

并不知道为啥内存不够了。。。使用 top 命令查看的时候 %MEM 那一栏大家都挺低的，但是就是可用内存很少。尝试重启了下各种程序发现并没有效果于是重启了 = = 大概现在正常了。

其实我五一假期放到 5.5 号所以大概这几天能修修 uoj 补补小 bug，有没有热心用户来吐吐槽呀？

………………我也没辙啊

如果你看到 UOJ 挂了多半就是被攻击了，超过一定流量阿里云会开启黑洞，切断服务器跟外界的连接，然后就没有人可以访问到 UOJ 了。

不知道是谁干的，最近被干了两次，峰值流量 10 GB。

可能想办 UOJ 这种小网站是挺难的吧，要是咱是个大公司就专门搞一大堆专业的 DDos 的防护了。

UPD： 3 次。

UPD： 4 次。（2017年2月8日）

UPD： 5 次。（2017年2月9日）

UPD： 6 次。时隔5年又来了，叹气。峰值流量 25 GB（2022年1月18日）

新年快乐！大家打得开不开心呀！

“一起AK吧”

长度测量鸡

from nneztlk

算法一

直接枚举刻度, 时间复杂度为 $O\left(\binom{n(n+1)/2-1}{n-1}\right)$. $n=5$ 时这个数是 $\binom{14}{4}=1001$, $n=8$ 时这个数是 $\binom{35}{7}=6724520$. 期望得分 $10\sim20$ 分.

算法二

我们需要题目描述中的 $s_j-s_i\ (0\le i< j\le n)$ 这 $\frac{n(n+1)}{2}$ 个数取到 $1\sim\frac{n(n+1)}{2}$ 的所有整数, 所以每个整数只能取一次, 即每种长度只能被一种方法量出. 特别地, $s_i-s_{i-1} (1\le i\le n)$ 这 $n$ 段长度两两不同, 故只能是 $1,2,\ldots,n$ 的一种排列.

枚举排列, 时间复杂度为 $O(n!)$. $n=8$ 时这个数是 $40320$. 期望得分 $20$ 分.

算法三

事实上, $n=1,2,3$ 时可以直接试出刻度方案, 分别为 $\varnothing,\{1\},\{1,4\}$, 而对所有 $n>3$ 都不存在满足要求的刻度. 证明如下:

记 $M=\frac{n(n+1)}{2}$, 则对 $n>3$, $M\ge10$. 现假设存在满足要求的刻度方案. 由于需要量出 $M-1$ 的长度, 所以 $1$ 或 $M-1$ 处必须有刻度, 由对称性不妨设 $1$ 处有. 要量出 $M-2$ 的长度, $2,M-2,M-1$ 中需要有一处有刻度, 而如果 $2$ 或 $M-1$ 处有刻度, 则可以用两种方法量出长度 $1$, 矛盾! 所以 $M-2$ 处必须有刻度. 此时由 $(M-2)-1=M-3$, $M-3$ 的长度已经可以被量出. 要量出 $M-4$ 的长度, $2,4,M-3,M-4$ 四处必有一处有刻度. 容易发现只有 $4$ 处的刻度不会引起重复.

现在已经知道 $1,4,M-2$ 处都需要有刻度, 而长度 $M-5$ 尚未被量出. 欲量出 $M-5$, 需要 $3,5,M-5,M-4,M-1$ 中的一处有刻度. 然而它们都会导致 $1,2,3$ 中的某个长度能被两种方法量出, 矛盾! 故不存在满足要求的刻度.

所以只需判断 $n$ 是否大于 $3$. 时间复杂度 $O(1)$, 期望得分 $100$ 分.

直径拆除鸡

from szy042

算法一

输出一朵花，就像 $(1, 2), (1, 3), (1, 4), \dots$

讲真这样子对于 $n \le 10$都是对的

然而当 $n = 11$ 时就开始挂啦

期望得分 20

算法二

输出一棵二叉树

（我没什么想说的

期望得分 $10$

结合算法一可以得30分

算法三

枚举树，按照题意模拟

找到一个最大的输出

UOJ的评测机很萌，所以能比算法一多十分~

期望得分：30

结合算法二，可以得40分

算法四 开花的金字塔

思考一下一棵树被删除一条长为x的直径之后的情况，我们发现，剩余的连通块中的直径最长为 $(\lfloor x/2 \rfloor-1) \times 2$。

证明是容易的。考虑这棵树原来的直径 $a$ 和删除之后最长的直径 $b$。我们取 $a,b$ 上最近的两个点 $c,d$，$c,d$ 两点把 $a$ 和 $b$ 分别分成两部分，各选取较长部分，加上 $c,d$ 之间的链，共同组成一条链，链长度的最小值就是 $\lfloor (a+1)/2 \rfloor + \lfloor (b+1)/2 \rfloor +1$，这条链的长度要小于原直径a，所以b不能大于 $(\lfloor a/2 \rfloor -1) \times 2$。

从取整符号可以看出，直径长度是偶数可以让 $b$ 最大，此时 $b=a-2$。

然后考虑一棵树被删除之后的连通块个数，除了最后一次删除，每多一个连通块，每个点被算入代价的次数显然会减少，于是就启发我们构造一个删除过程中不出现新的连通块的图，与上面的删除直径相联系，我们就可以随手构造一个符合条件的图出来。

将节点数分别为 $1,3,5,7,\dots$ 的链的中点相连，这就是一个符合要求的图。什么？你问多出来的那些点怎么办？扔到长度为 $3$ 的链的中点上（前面的字数太多于是后文称之为天上），变成一座开花的金字塔。考虑这些多出来的点对代价的贡献，放到天上的正确性是显然的。

期望得分：50

结合算法一/三可以得到60

算法五

我们发现算法四还需要结合算法一/三才能获得 60 分，因为算法四没有办法通过 $n=9$ 的测试点，于是，我们发现链的条数不是越多越好。因为一方面，链数增多可以让天上的结点的递归层数增加，但另一方面链数增多需要囤积更多的递归层数很浅的结点。所以我们需要枚举链的条数，将多出来的扔到天上，如果结果大于 $m$，输出之。

期望得分 100。

啊严谨证明是：用 $f[n][p]$ 表示有 $n$ 个节点直径长度为 $p$ 的最多删除次数，用前面得到的删除一条直径后的直径长度关于 $p$ 的不等式搞一搞，就能列个递推式。可以用数学归纳法证明 $f[n][p] = kn - b$，其中 $k$ 和 $b$ 是某个关于 $p$ 的常数。观察 DP 的取值，就能反向构造出对应的最优解了，发现恰好就是上面那样是最优的。

快乐游戏鸡

from scPointer

算法一

注意到当当前死亡次数不变的时候，整棵树上可走的点和边也是不变的。 考虑把每个点拆成 $ \max \{w_i\} $个点，然后跑分层图就好了。

或者你可以设一个状态 $f[i][j]$ 表示死亡 $i$ 次，当前在结点 $j$ 的最短时间然后跑dp。

后者的复杂度是 $O(nq\max \{w_i\})$ 的。这样可以通过子任务 $1$ 拿到 $10$ 分。

算法二

你可以发现每次从点 $s$ 出生到撞程序猿死亡跟前几次是怎么死的并没有关系。所以对于每次 “从点 $s$ 出生到撞程序猿死亡” 的过程都可以贪心选最近的点早死早超生。如果暴力BFS贪心的话复杂度是会炸的，离散化权值也不行。

我们换个角度，考虑有多少次从出生到死亡的过程需要一秒，多少次需要两秒等等。

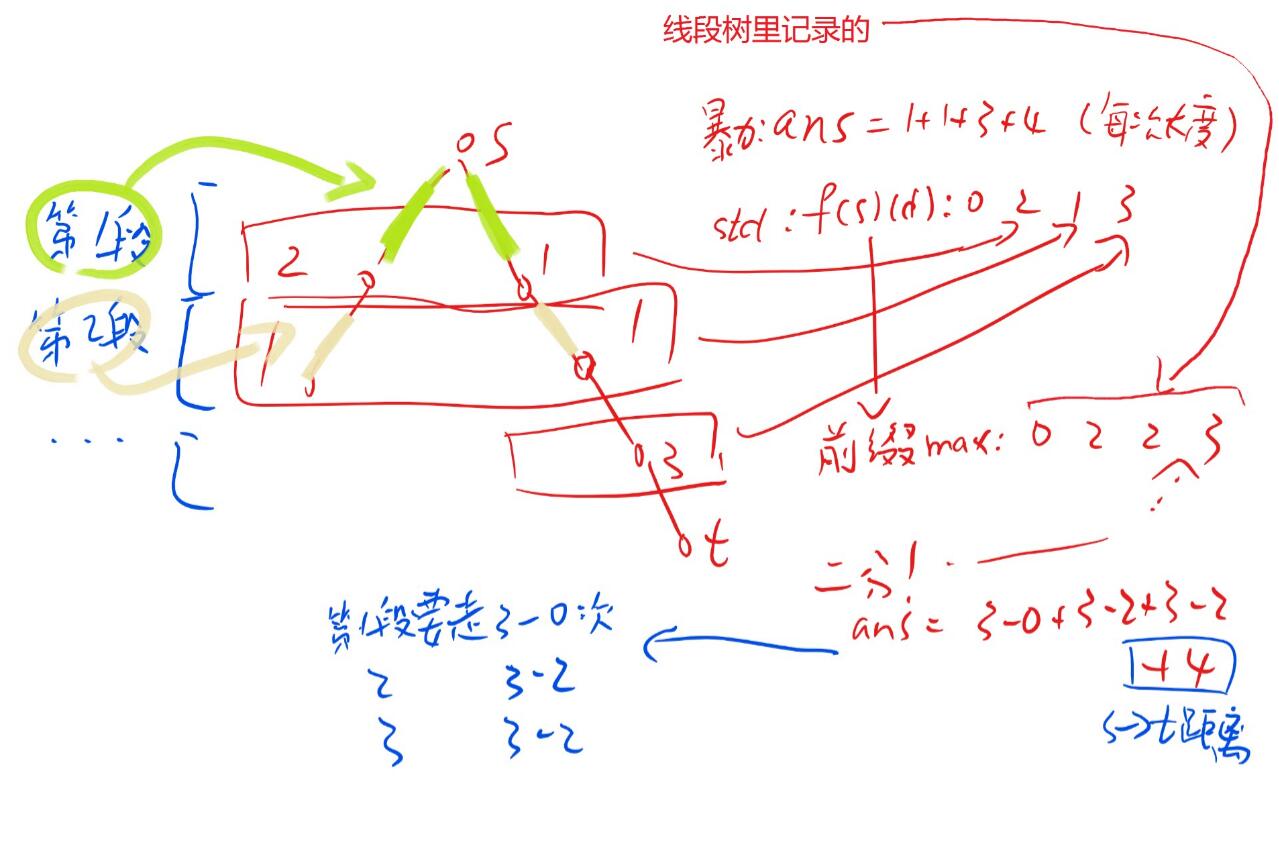
具体来说，考虑记录 $f[i][j]$ 表示 $i$ 的子树中和 $i$ 距离小于等于 $j$ 的点的权值最大值。 这样 $f[i][j]-f[i][j-1]$ 就等于有多少次从出生到死亡需要 $j$ 秒。 那么只要从 $0$ 开始枚举 $j$ 把贡献加起来，直到 $s$ 和 $t$ 联通的时候直接从 $s$ 走到 $t$ 就好了。

复杂度 $O(n^2+nq)$ ，可以通过子任务 $1,2$ 拿到 $20$ 分。

算法三

算法3-1

因为所有 $s=1$ 所以就可以把算法 $2$ 里 $f$ 的第一维删掉辣。然后把 $f$ 搞搞差分前缀和什么的，每次询问二分就好了。复杂度 $O(n+qlogn)$ 。

算法3-2

或者...让我们回到算法二的第一段。如果你只想到贪心没有想到记录 $f$ 数组，那么第三个部分分也是可以拿的。首先对询问的每个终点按照能到达那个终点的死亡次数排序，然后算法二第一段的贪心过程可以用一个堆或者set来做。

如果一个点可以被到达（可以安全通过它的父亲了），就扔进来，如果死亡次数大于等于某个点的权值（可以安全通过它自己了），就扔出去。当前死亡次数达到某个点的死亡次数的时候就处理一下询问就好了。复杂度 $O(q+nlogn)$ 。

这两个算法和场上可能出现的各种我可能没想过的算法可以通过子任务 $3$ ，这样就有 $40$ 分了。

算法四

算法4-1

为了方便叙述，我们把点 $1$ 放在最左边，点 $n$ 放在最右边，拉成一条链。

然后把所有询问按照左端点从右向左排序，处理 $f$ 数组的时候也从右向左处理。然后观察一下每次往左扩展一个点的时候 $f$ 数组有啥变化，然后你机制的发现这个是可以用线段树转移的，询问也可以在线段树上查询。

等一下！每次加一个点的时候好像是区间对一个数取max唉，是不是要强上一波segment tree beats(吉司机线段树)啊。如果是场上真的有选手卡在这里的话，我表示非(xiao)常(chu)遗(sheng)憾。回到算法 $2$ 看一眼 $f$ 的定义你会发现这玩意是单调递增的，所以我们二分出线段树上最后一个小于要更新的那个数的地方，然后区间覆盖就可以了。

稍微剧透一下兹磁区间覆盖和区间求和的线段树就可以最终解决问题。复杂度 $O((n+q)logn)$ 。

算法4-2

首先还是从右往左处理所有东西。注意到当处理到点 $i$ 的时候，如果存在 $i < j < k$ 使得 $w_j \geq w_k$ 那么我们肯定不可能死在 $k$ 点。

如果把所有这样的点删掉，我们就得到了一个单调栈！然后每次往左扩展一个点就维护一下，询问直接二分就好。注意当删掉一些点以后相当于边权可能会 $>1$ ，加减乘除处理一下就好。 稍微剧透一下你可能需要维护后缀和。复杂度 $O(n+qlogn)$ 。

这两个算法可以通过子任务 $4$ ，或者一些大力出奇迹的算法可能也能过，这样就有 $70$ 分了。

算法五

算法5-1

大致和算法4-1差不多，加上树链剖分和启发式合并的话就能直接做了。代码可能会有一点长。

什么你说不会做？如果能写出4-1的代码，你肯定已经知道了如何往一棵线段树上加一个点更新信息。然后树链剖分以后对于每个点，首先把它的重儿子的线段树拉过来更新一下，然后对于它的每个轻儿子的重链（注意不是轻儿子的子树，否则可能复杂度会多一个log有卡常风险）对应的线段树拉过来更新当前点的线段树就好了。推荐按照树剖的DFS序建一棵线段树，然后上面提到的所有操作都可以在这一棵线段树上做。复杂度 $O((n+q)logn)$ 。

算法5-2

同算法4-2,同样是加上树链剖分和启发式合并搞一搞。复杂度 $O(n+qlogn)$ 。详见xllend3大爷的代码

算法5-?

这题还有很多做法，比如你不喜欢用普通线段树换成动态开点的线段树或者可持久化线段树或者treap什么的也是可以的。当然复杂度和常数就要自己保证了。myy似乎提了一个按权值建LCT的做法：http://matthew99.blog.uoj.ac/blog/2296

数据分块鸡

from jiry_2，数据和题解 from cy

子任务一

设 $f[i]$ 表示最后一个分块点是 $i$ 的最小代价，那么我们转移时可以枚举上一个点 $j$，然后令 $f[i] = \min\{f[j] + w(j, i)\}$，其中 $w(l, r)$ 表示与 $[l, r)$ 相交的询问所产生的代价。

时间复杂度：$O(n^2 q)$。

子任务二

我们可以尝试预处理 $w$ 函数的所有取值。

设 $g[l][r] = w(l, r)$，那么对于一个询问 $[L, R)$, 我们可以根据 $[l, r)$ 与 $[L, R)$ 的相交情况大力讨论一发，拆成把若干个 $g$ 数组的子矩形加上某个数，这可以离线前缀和一下。时间复杂度是 $O(q + n^2)$ 的。

预处理完之后 DP 的复杂度就变成 $O(n^2)$ 了，于是总的复杂度是 $O(q + n^2)$。

子任务四

通过数（da）学（dan）证（cai）明（xiang）我们发现，这个 DP 满足决策单调性。

于是我们可以采用对于满足决策单调性的 DP 的通用做法：在 DP 的同时维护一个单调栈，转移的时候在栈上二分一下得到最优决策点。

计算 $w(l, r)$ 可以通过按照 $[L, R)$ 与 $[l, r)$ 的相交情况分类讨论，拆成对若干个子矩形求和，并用可持久化线段树预处理这些前缀和。

时间复杂度：$O(n \log^2 n)$。

子任务三

通过更进一步的分析，我们可以证明分界点只有可能是 $l_i$，$l_i - 1$，$l_i + 1$ 或 $r_i$，$r_i - 1$，$r_i + 1$。因此我们可以只把这些点拿出来 DP。

时间复杂度：$O(q^3)$。

同构判定鸡

from ppfdd，具体想法 from vfleaking，题解也是 vfleaking 写的。

题出得比较仓促，所以测试点只有 $6$ 个……窝先说一下……窝最初的想法是 “哇终于知道怎么出交互式证明的题了！”，然而造题的过程是：

YY 一个图同构算法 → 不会卡 → 再 YY 一个图同构算法 → 还是不会 → 要不咸鱼一下爆搜看看效果如何 → 那不就从构造题变成爆搜题了，不清真 → 继续 YY……

由于我太弱了所以测试点也比较弱，大家玩得开心就好。

卡算法一

算法一：仅检查结点数及边数是否一致。

直接扔个点数边数相同的两个不同构的图就行了，可以获得 $7$ 分。

卡算法二

算法二：首先仅检查结点数及边数，然后结点数很小时使用暴力，否则视为同构。

在卡算法一的基础上造个大一点的图。

卡算法三

算法三：初始每个结点颜色相同，每次对于每个结点结合自身的颜色和周围邻居的颜色编码产生新的颜色，反复迭代直至稳定。将最后每个图所得颜色进行排序，若相同则视为同构。

废话好多！直接扔两个度数相同的图就行了。

卡算法四

算法四：与算法 3 类似，只是用结点间最短距离信息初始化结点颜色。

有两个方法。一个方法是人类智慧构造一下。首先仿照卡算法三的思路，这个图最好是每个结点的距离数组都长得一模一样。那么考虑把大家围成一个圆圈尝试有规律地连边，试了下最后竟然成功了。

A：$6$ 个点，$i$ 与 $(i + 1) \bmod 6$ 连边，$i$ 与 $(i + 3) \bmod 6$ 连边。

B：$6$ 个点，$i$ 与 $(i + 2) \bmod 6$ 连边，$i$ 与 $(i + 3) \bmod 6$ 连边。

这样构造发现恰好是满足的，就可以同时卡掉算法一二三四了。

还有另一个构造，方法是找两个不同构且每个点度数都相同的图，分别新建一个点向所有点连边。这样其实原图中没有边相连的两个点距离就为 $2$，有边即为 $1$。这样的构造也是可以骗过算法四的。

另一个方法：大爆搜所有无向图，搜到 $n = 6$ 就能找到上面的这个构造了……

卡算法五

算法五：枚举一个图中的一个固定的结点与另一个图中哪个结点对应，将他们分别染成特殊的颜色，其它结点颜色照常初始化，再用算法 3 中的迭代。若存在一种对应使得最后所得颜色相同，则视为同构。

只用在卡算法四的基础上往前面插入一个编号为 1 号点向所有其他点连边就行了，这样给这个点特殊染色不会带来任何信息。

另一个方法：大爆搜所有无向图，搜到 $n = 7$ 就能找到上面的这个构造了……

卡算法六

算法六：一种基于邻接矩阵的整数次幂的迹的哈希算法

啊发现哈希好难卡……发现哈希的模数是 int 范围的。考虑用爆搜来构造。

但是要怎么快速生成很多个满足前 5 个算法的图呢？

可以这样想：算法五里引入的这个向所有点连边的点不会带来任何信息，所以多加几个这样的点也肯定满足题目条件。而且进一步考虑在这样的新点之间连边，如果连边方式一致，那么同样也不会给那个 $6$ 点图带来任何信息。

所以我们可以在卡算法四的基础上，给 $A, B$ 加一大堆新点出来，然后随机连边。但是这样大约需要随机 $O(M)$ 次才能随机到相同的哈希值。

这个哈希函数实在是算得太慢了，GG 怎么办呢。如果用生日攻击的话，那么模数是 $M$ 期望 $O(\sqrt{M})$ 个样本就能卡了。

然而我们可以结合卡算法四中的第二个构造。把新点随机成点度数相等的图就好了。由于 $A, B$ 不同构所以我们可以直接随机不用判断是否随机到了同构的图。

当然场上有一位机智 bzoj 给出了一个直接的构造：在这里 太强了……QAQ……

终极武器

好吧虽然不是想鼓励大家这样做，但是可能很有效。上网搜“graph isomorphism counter example”，可以得到一些奥妙重重的卡图同构算法的反例。下载一些下来喂进交互库说不定哪个就成功了。囧rz……以后出题还是要注意注意别出这种能 google 的题。

嗨呀以及感觉这次的题目总体还是偏难，感谢大家参赛啦！

再见，丙申！

转眼间 2016 年也过去了，然而在过去的一年里，我们可爱的计算鸡每天都要惨遭野蛮的程序猿欺负。

在程序猿的敲打下，计算鸡被迫写下了许多时而有空格时而没空格、大括号时而换行时而不换行，甚至还有用记事本写出来的 C++ 代码。

终于到了除夕这一天，计算鸡们发怒了。计算鸡村村长垫子计算鸡，召集了全村上下所有的计算公鸡、计算母鸡、计算鸡中的战斗鸡等广大鸡类群众，接着成千上万的计算鸡愤怒地向程序猿的栖息地涌去！

然而垫子计算鸡还不知道，真正的敌人是默默操纵整个世界已有一年之久的猴族首领猴腮雷，一场大战即将拉开。

我们将于除夕前一天下午 13:00 到 18:00 举办一场盛大的 Goodbye Bingshen 赛。

即：1月26日下午 13:00 到 18:00。注意此次比赛时间为 5 小时，共 5 道题 ABCDE 来给大家贺岁～

赛制仍然是OI赛制，但是题目难度嘛，水题和省选难度题兼有。欢迎所有人包括萌萌哒NOIP选手来玩！

出题人：nneztlk, szy042, scPointer, jiry_2, ppfdd

这场成绩将计入rating。

参加本次比赛将有机会获得 UOJ 抱枕！3af40cb9a16abb337db27feca1c2c0c1 是获奖条件的 md5 码。比赛结束后将公布条件。

再次提醒大家比赛中途只测样例，最后会进行最终测试，把所有提交记录重测。

UPD： 比赛已经结束！

echo -n 比赛开始2016s后的第一个提交 | md5sum
3af40cb9a16abb337db27feca1c2c0c1

恭喜获得前 5 名的选手！

1. Dylan_Sun
2. WrongAnswer
3. sjj118
4. xyz2606
5. JOHNKRAM

恭喜 Austin_Griffin 获得 UOJ 抱枕一个！

UOJ Test Round #2 将于 1 月 8 日星期日晚上 19：00 举行！比赛将进行 3 个小时，共三道题。

话说 vfk 开学之后对于 UOJ 甩锅已久，很久没有比赛了，投到 UOJ 的题目又频频被管理员们秒掉……

这可怎么办呢？

看了看最近的 UER/UR 的难度，UR 赛制只有 3 小时，题目太难大家不肯捉 —— 于是我们决定降低下题目的难度，嗯……然后我们瞬间就有三道题出了！

这次 Test Round 一方面是为了测试降低难度的 round 大家捉起来感觉怎么样，另一方面是为了测试即将上线的比赛问答系统。

（咳咳大家这次在切题的时候一定要记得调戏下比赛问答系统，可以对题意不清的地方提问，出题人会进行回答哒）

本次比赛将以“出题”为主题。

出题人：jiry_2, jiry_2, jiry_2

如果新功能没出问题的话，这场成绩将计入rating。

参加本次比赛将有机会获得 UOJ 抱枕！5d1ee77c1c495a6303e781cbe002b61b 是获奖条件的 md5 码。比赛结束后将公布条件。（你猜抱枕跟比赛问答系统有没有关系呀？）

再次提醒大家比赛中途只测样例，最后会进行最终测试，把所有提交记录重测。

（其实感觉这次难度确实好水好水，大家捉得开心就好）

UPD： 比赛已经结束！

echo -n 比赛中最后一个提问的 | md5sum
5d1ee77c1c495a6303e781cbe002b61b

恭喜获得前 5 名的选手！

1. Rui
2. owaski
3. xumingkuan
4. 613
5. philipsweng

恭喜 sqc 获得 UOJ 抱枕一个！

很久很久以前，vfk 说：“UOJ 要开源”

然后……vfk 打开了 UOJ 的代码……发现好大一口锅

于是 vfk 开始整代码整代码，配环境配环境……终于！今天 UOJ 开源了！

丢链接跑：

https://github.com/vfleaking/uoj

搞下来然后根据安装小教程搞一发就行了。封在 docker 里的，linux 和 mac 上应该挺好装的，不过 windows 用户得难受一下了hhh……

由于之前基本上是我一个人开发，当然还有 cyb 和 ljc 帮忙……但是……

什么没有文档？传题的文档还是有的。

什么没有注释？被注释掉的代码还是有的。

什么时候更新一波文档啊？看大家开发热情！这次发布之后我会写一波嗯。

这次开源的目的是为了 UOJ 的代码能够继续发展下去，把一些锅比如 “博客的个人主页” 通过大家的力量给填上。当然对于大家来说，又多了一个 hustoj 一样的存在，可以在学校的服务器上轻松搭一个校内的 UOJ。想用 ptrace 写沙箱的码农们，UOJ 的沙箱也是一个很好的参考。

以及！！！如果发现了任何 bug 求不要 hack 线上的 UOJ……QAQ……UOJ 的题目数据其实是公开的，写程序弃疗了可以伸手找找管理员要一份，除此之外 hack 网站也没啥吸引力对不……QAQ……发现了 bug 请尽快通知我们，非常感谢。

联系方式：uojmanagers@groups.163.com 或 vfleaking@163.com。

最后丢群跑：Universal OJ 开源群，590822951。想研究源码以及安装有困难的各位，在群里多交流哈～

嗯最后，祝大家 UOJ 使用愉快！愿 UOJ 开源能带来更多的便利，愿能帮到更多还在路上的 OIer 们。

（咳咳 UOJ 用户群里的某些人应该改群名片了）

奥林匹克五子棋

from qmqmqm

算法一

答案只与最后的棋盘有关。暴力枚举所有的棋盘然后判断是不是符合条件。

最终复杂度是 $O(nm2^{nm})$。可以获得 30 分。

算法二

如果对于一组 $n,m,k$ 如果有解，那么对于 $n,m,k+1$ 也有解。

明显如果 $k=1$，那先手随便下一个子就赢了，所以无解。

当 $\min(n,m)=1$ 时，如果 $k=2$,那么双方只要棋子间隔分布，就是可行解。

最终复杂度是 $O(nm)$。可以获得 15 分。

算法三

当 $\min(n,m) \lt k$ 时，斜线方向是明显永远符合条件的。所以我们采取像黑白染色那样，这样在横竖方向上最长连续段都是 $1$，明显是符合条件的解。

最终复杂度是 $O(nm)$。可以获得 15 分。

算法四

当 $n,m \geq 2$ 时，可以证明如果 $k=2$ 是无解的。

具体来说考虑 $(1,1),(1,2),(2,2)$ 三个点，由抽屉原理得其中必定有两个点同色，那么他们就成了一个长为 $2$ 的同色连续段。

所以我们来考虑 $k=3$ 的情况。

可以想到，$k=3$ 一定不会在内部有一个 $2 \times 2$ 的同色块，否则这个块的下方三个位置就会形成一个长为 $3$ 的同色连续段。进而一个同色的 L 形也不能存在，因为其上方三个斜向位置都必须和它颜色不同，从而形成一个长为$3$的同色连续段。

这样一来，构造必须是一些 $1 \times 2$ 的条间隔分布。观察发现，这个构造符合题目中的所有条件。再根据上边的结论，$k \gt 3$ 的情况也解决了。

最终复杂度是 $O(nm)$。结合算法二可以获得 100 分。

奥林匹克环城马拉松

from ftiasch，题解 from C_SUNSHINE

算法一

首先我们判断掉无解的情况，即存在一个点度数为奇数，此时方案数为 $0$。

从 $1$ 号点开始搜索欧拉回路，只要记录当前在哪和 $u,v$ 之间还有几条边没有走就好了，状态数是所有 $t_i$ 的积乘以 $n$，每次枚举下一步往哪走，可以从将要走的路上选一条未走过的边来走，并乘以这条路上剩余的边数，这样转移复杂度是 $O(n)$ 的，可以得到 $20$ 分。

算法二

注意到树的每一条边数目都是偶数，且走过去和走回来的次数各占一半，令一个点的度数 $deg_x$ 为走入这个点的次数即这个点相邻边权和除以$2$。

首先先要确定每一条边的方向，这个其实就是在每一组重边中选一半向下，另一半向上，所以是 $\prod \binom{t_i}{t_i/2}$。

那么确定方向之后，欧拉回路如何计数呢？

我们有一个简单粗暴的方法，在每个点上对于每一条入边为它指定一个后继出边，这样边与边之间就连起来了，由于 $deg_x$ 条入边和出边的匹配方案数是 $deg_x!$，于是答案就是 $\prod deg_x!$。

妈呀我怎么过不了样例啊……

可以发现这样确定出来的不是欧拉回路，而是若干个环并在一起。

继续思考，我们可以使用一些类似“骨架”的东西来连接整个欧拉回路。而在连通图中，树是一个不错的选择。

我们令欧拉回路从 $1$ 号点开始走，把最后一次经过除 $1$ 号点以外的点时走的出边拿出来作为特殊边。那么除了 $1$ 号节点以外每个节点有一条出边，并且由于是最后一次，不会出现环。于是这些特殊边构成了一棵以 $1$ 为根的树。

怎么统计这棵树呢？只要从向上走的边上拉一条出来就好了，方案数是 $\prod t_i/2$

确定了最后一条出边之后找欧拉回路的过程其实也不难，对于一个点 $x(x>1)$，前 $deg_x-1$ 次可以非特殊出边中任意挑选，最后一次只能走特殊出边，方案数是 $(deg_x-1)!$。对于 $1$ 号点来说没有特殊边的限制方案数仍然是 $deg_1!$。

于是方案数变成了 $deg_1!\prod_{x>2} (deg_x-1)!$，再乘上其他系数……妈呀我怎么还是过不了样例啊。

注意题目要求循环同构算同一种方案，但是你强制起点是 $1$，而 $1$ 在欧拉序列中可能出现了多次，于是你就统计了多次。

解决办法也很简单，$1$ 在欧拉序列中出现的次数恰好是 $deg_1$，除掉即可，这样最后一部分方案数变成了 $\prod (deg_x-1)!$。

时间复杂度 $O(n)$，期望得分 $20$ 分，结合算法一可获得 $40$ 分。

算法三

观察树上的结论，我们会发现有向图的欧拉回路计数问题是有一个通用公式的：

$$T \cdot \prod (deg_x-1)!$$

其中 $T$ 是以某个节点为根的树形图数目。

于是问题就变成了给图定向。

考虑一个环的情况，由于 $t_i \leq 10^4$，我们可以直接枚举在环上转了几圈，那么每条边往两个方向走的次数都能计算出来。

接下来就是求环的树形图数目了。

对于 $n=m=3$ 的情况显然可以手算，其余的情况，注意到树只比环少一条边，那么枚举那条边断开就好了。

时间复杂度 $O(t_in)$，期望得分 $30$，结合算法一二可获得 $70$ 分。

算法四

环的问题解决之后，环套树问题就变得十分容易了。事实上，枚举任意一条环边正着走了多少次，根据有向图欧拉序列条件式 $indegree_x=outdegree_x$，就可以直接给无向边定向，定向的方案数直接用组合数计算就好了，例如 $t_i$ 条无向边有一侧是 $s_i$ 条，方案数就是 $\prod \binom{s_i}{t_i}$。

第二步就是树形图计数，这一步只要把环上的树形图计数和每个点的外向树树形图计数直接乘起来即可。

最后乘以 $\prod (deg_x-1)!$ 即可。

时间复杂度 $O(t_in)$，期望得分 $100$ 分。

奥林匹克数据结构

from ppfdd，题解 from matthew99

算法一

直接按照题意模拟，时间复杂度$O(n\sum{{m_i} ^ 2})$，加上一些小优化很容易做到$O(n\sum{m_i})$。

算法二

考虑KMP的过程，我们同样考虑对b串建出KMP中的fail数组。那么我们发现，只需要将KMP中判断两个数相等的操作改成判断只要最后一个数字在整个序列中的名次相同即可。

用主席树实现可能会有常数问题。我们发现，我们只需要用树状数组预处理出b串中每个位置在它前面的所有数中的名次。然后再用树状数组维护当前的border，由于在KMP中border是单调的，所以每次border变化的时候暴力修改即可。

时间复杂度$O((n + \sum{m_i})\log{n} + \sum{m_i\log{m_i}})$。

算法三

考虑多串匹配，显然就是将KMP改成AC自动机，转移就是考虑下一个数在当前点到根的路径上的所有数中的名次，现在由于没有类似KMP的border的单调性，我们必须用主席树维护了。注意实现的时候，每次失配时一定要顺着fail链走上去而不是直接将转移置为fail节点的对应转移，否则会由于字符集太大无法保证复杂度（注意如果是一棵普通的trie而且字符集很小，一定要将转移置为fail节点的对应转移，因为普通trie的叶子节点深度之和可能很大）。

接着将原串在AC自动机上走一遍，最后更新子树和。注意如果暴力更新子树和会由于复杂度不对而超时。

注意要用平衡树或者hash存储转移。

时间复杂度$O(n(\log{n} + \log{q}) + \sum{m_i\log{m_i}})$。（$q$是因为AC自动机上每个点度数最多是$q$）

算法四

注意到如果$\max{m_i} \le 25$，我们可以对于长度小于$\max{m_i}$的串全部预处理一遍hash值并存下来，具体来说可以存在一个数组里面然后排序，然后询问的时候直接二分查询个数即可。

用树状数组加上异或哈希实现常数较小，可以通过四个$\max{m_i} \le 25$的点。

时间复杂度$O(n\max{m_i}\log{n} + q\log(n \max{m_i}))$。

算法五

我们考虑在线怎么做。对于普通的字符串，这个问题显然是用后缀三兄弟或后缀平衡树解决。那么在这个问题上是不是也可以如此呢？

后缀数组！

慢着……这玩意儿。。。后缀数组要求把后缀进行排序，很好，两个名次数组怎么比较顺序？

后缀自动机！

慢着……这玩意儿。。。一个结点能识别的子串的长度都不固定，怎么玩？

后缀平衡树！

慢着……这玩意儿。。。还是不知怎么比较两个名次数组的顺序啊。

后缀树！

慢着……这玩意儿。。。诶不慢，好像可以。

考虑用Ukkonen算法构造后缀树的过程，显然每一步也很容易用主席树推广到这题上。

然而直接用 Ukkonen 算法会被卡复杂度。我们把孩子数不等于 $1$ 的非根节点称为特殊节点，原因是在普通串上，一个特殊节点的后缀链接显然会指向一个特殊节点，因为特殊节点已经有两个不同的字母作为转移，那么它的后缀链接肯定也有这两种字母，而在本题中不然，由于后缀链接指向了一个更浅的点，因此两种转移可能会合并为一个。

解决方法很简单，在找后缀链接的时候，如果它的父亲不是特殊节点，那就找它父亲的父亲，直到找到一个特殊节点，再从那个特殊节点开始求出当前点的后缀链接，可以证明这样的复杂度是正确的。

构造完后缀树之后求一遍子树和，每次在后缀树上跑一边查询即可。

时间复杂度 $O(n \log n + \sum{m_i(\log{m_i} + \log{n})})$。

有人说，有后缀数组和后缀自动机了，还要后缀树干嘛？从这题可以看出，每个数据结构都有自己的特性。后缀树在这题上能够成功的原因，也许是因为他其实是某种后缀 Trie 的 AC 自动机吧。而 AC 自动机能够解决离线问题的原因，也许是因为他其实是推广后的 KMP 吧。这一切，也许正是奥林匹克数据结构的魅力所在。

光阴似箭，日月如梭，软件在更新，时代在进步！（喂喂）

现在 UOJ 的 C/C++ 编译器闷声从 gcc-4.8.2 和 g++-4.8.2 升级到 gcc-4.8.4 和 g++-4.8.4 了！不过其实都第三位版本号了，没多大差别了……

（其实之前用在清华集训、清华校赛、清华夏令营的那版校内 UOJ 的编译器就是 4.8.4 的，不知大家注意到没有）

咳咳，因此测评时间在2016年8月8日以前的为旧编译器的测评结果，2016年8月8日及之后的为新编译器的测评结果。

最后播送一则谣言：坊间传说几年内 OI 系列比赛将取消 Pascal，嗯……画面真美不敢想象……那时候出交互题就可以少写一种交互库了哈哈哈……（别问我是不是真的）

好，今天的 UOJ 新闻联播就到这里！